抽象地说，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。

站在回溯树的一个节点上，你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

回溯算法的框架：
#

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。

[!warning] 与 DFS 算法的区别就是「做选择」和「撤销选择」到底在 for 循环外面还是里面的区别，DFS 算法在外面，回溯算法在里面。

[!tip] 划重点动归/DFS/回溯算法都可以看做二叉树问题的扩展，只是它们的关注点不同：
动态规划算法属于分解问题（分治）的思路，它的关注点在整棵「子树」。
回溯算法属于遍历的思路，它的关注点在节点间的「树枝」。
DFS 算法属于遍历的思路，它的关注点在单个「节点」。

例子：
#

全排列算法

![[Pasted image 20250223173155.jpg]]

分析
#

只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。

为啥说这是决策树呢，因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上：

你现在就在做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在你身后，这个选择你之前做过了，而全排列是不允许重复使用数字的。

现在可以解答开头的几个名词：[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候。

如果明白了这几个名词，可以把「路径」和「选择」列表作为决策树上每个节点的属性，比如下图列出了几个蓝色节点的属性：

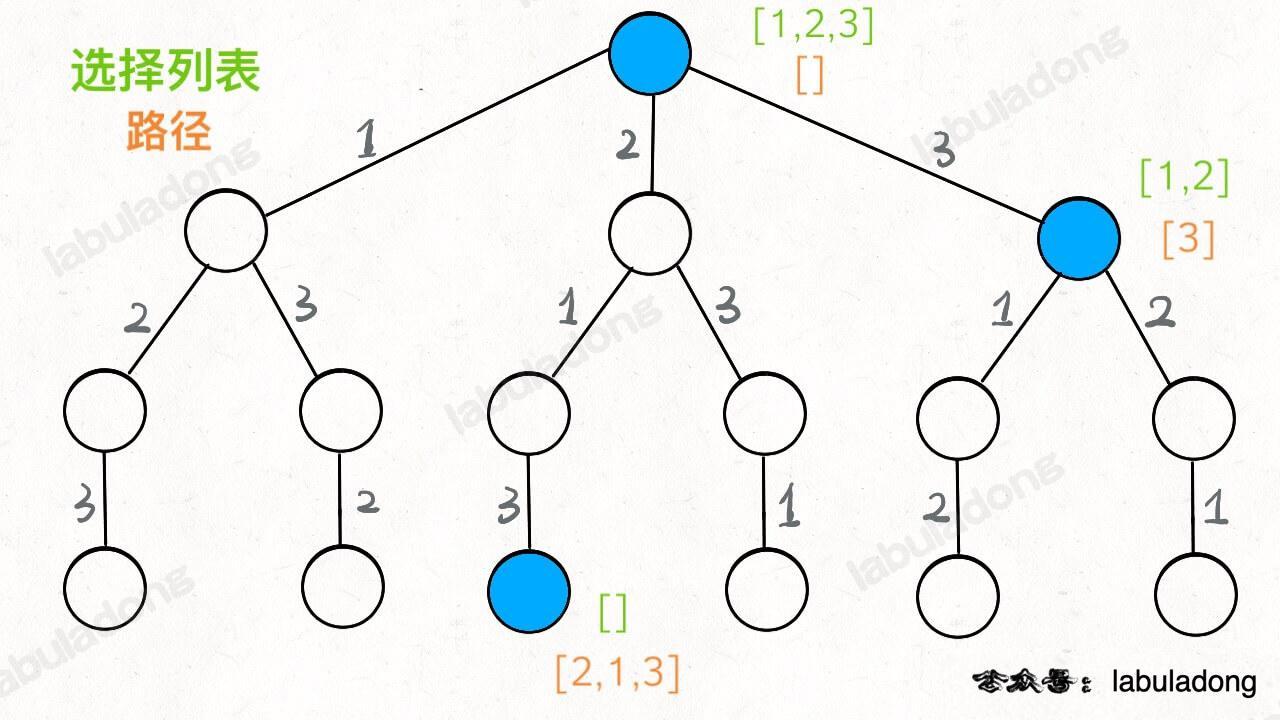
我们定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层叶子节点，其「路径」就是一个全排列。![[Pasted image 20250223173357.jpg]]

代码
#

from typing import List

class Solution:
    def __init__(self):
        self.res = []

    # 主函数，输入一组不重复的数字，返回它们的全排列
    def permute(self, nums: List[int]) -> List[List[int]]:
        # 记录「路径」
        track = []
        # 「路径」中的元素会被标记为 true，避免重复使用
        used = [False] * len(nums)

        self.backtrack(nums, track, used)
        return self.res

    # 路径：记录在 track 中
    # 选择列表：nums 中不存在于 track 的那些元素（used[i] 为 false）
    # 结束条件：nums 中的元素全都在 track 中出现
    def backtrack(self, nums: List[int], track: List[int], used: List[bool]):
        # 触发结束条件
        if len(track) == len(nums):
            self.res.append(track.copy())
            return

        for i in range(len(nums)):
            # 排除不合法的选择
            if used[i]:
                # nums[i] 已经在 track 中，跳过
                continue
            # 做选择
            track.append(nums[i])
            used[i] = True
            # 进入下一层决策树
            self.backtrack(nums, track, used)
            # 取消选择
            track.pop()
            used[i] = False