二叉树算法纲领

#

先在开头总结一下，二叉树解题的思维模式分两类：

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个  traverse  函数配合外部变量来实现，这叫「遍历」的思维模式。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论使用哪种思维模式，你都需要思考：

如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

深入理解前中后序

#

我先甩给你几个问题，请默默思考 30 秒：

1、你理解的二叉树的前中后序遍历是什么，仅仅是三个顺序不同的 List 吗？

2、请分析，后序遍历有什么特殊之处？

3、请分析，为什么多叉树没有中序遍历？

答不上来，说明你对前中后序的理解仅仅局限于教科书，不过没关系，我用类比的方式解释一下我眼中的前中后序遍历。

首先，回顾一下二叉树递归遍历框架：

def traverse(root):
    if root is None:
        return
    # 前序位置
    traverse(root.left)
    # 中序位置
    traverse(root.right)
    # 后序位置

先不管所谓前中后序，单看  traverse  函数，你说它在做什么事情？

其实它就是一个能够遍历二叉树所有节点的一个函数，和你遍历数组或者链表本质上没有区别：

单链表和数组的遍历可以是迭代的，也可以是递归的，二叉树这种结构无非就是二叉链表，它没办法简单改写成 for 循环的迭代形式，所以我们遍历二叉树一般都使用递归形式。

你也注意到了，只要是递归形式的遍历，都可以有前序位置和后序位置，分别在递归之前和递归之后。

所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，那么进一步，你把代码写在不同位置，代码执行的时机也不同：

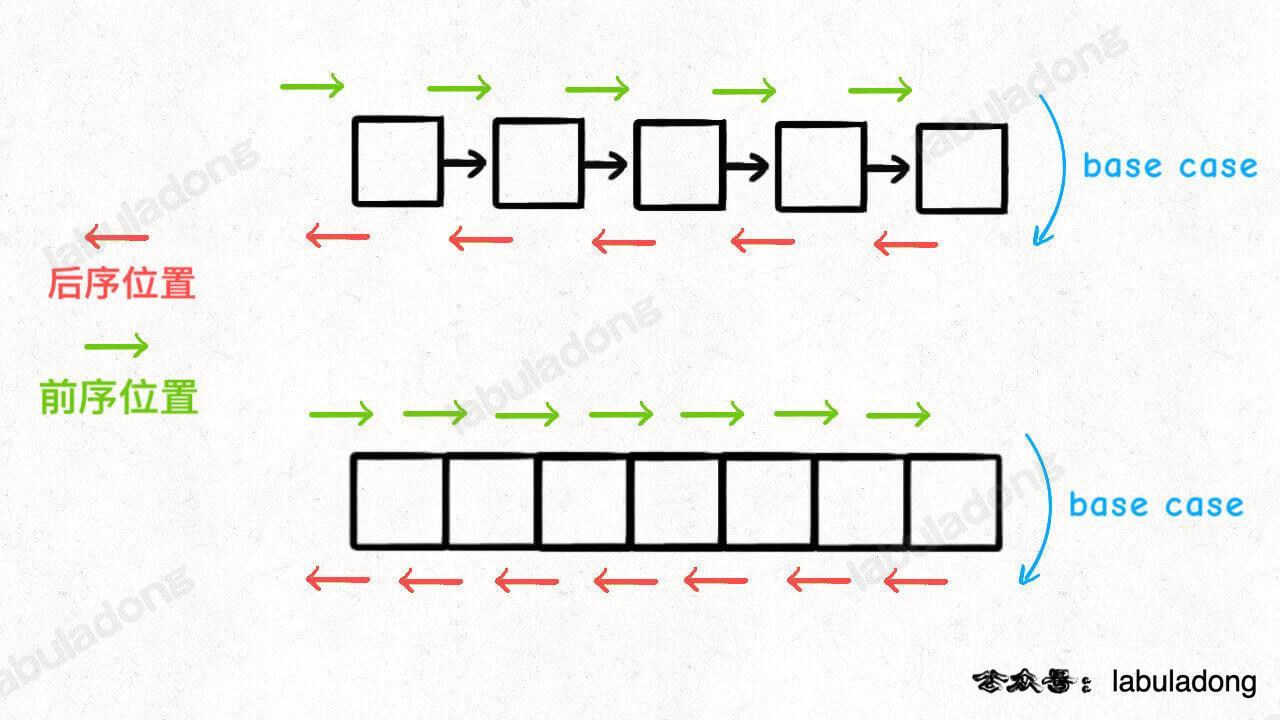
比如说，如果让你倒序打印一条单链表上所有节点的值，你怎么搞？

实现方式当然有很多，但如果你对递归的理解足够透彻，可以利用后序位置来操作：

# 递归遍历单链表，倒序打印链表元素
def traverse(head):
    if head is None:
        return
    traverse(head.next)
    # 后序位置
    print(head.val)

结合上面那张图，你应该知道为什么这段代码能够倒序打印单链表了吧，本质上是利用递归的堆栈帮你实现了倒序遍历的效果。

那么说回二叉树也是一样的，只不过多了一个中序位置罢了。

教科书里只会问你前中后序遍历结果分别是什么，所以对于一个只上过大学数据结构课程的人来说，他大概以为二叉树的前中后序只不过对应三种顺序不同的  List<Integer>  列表。

但是我想说，前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List：

前序位置的代码在刚刚进入一个二叉树节点的时候执行；

后序位置的代码在将要离开一个二叉树节点的时候执行；

中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

你注意本文的用词，我一直说前中后序「位置」，就是要和大家常说的前中后序「遍历」有所区别：你可以在前序位置写代码往一个 List 里面塞元素，那最后得到的就是前序遍历结果；但并不是说你就不可以写更复杂的代码做更复杂的事。

画成图，前中后序三个位置在二叉树上是这样：

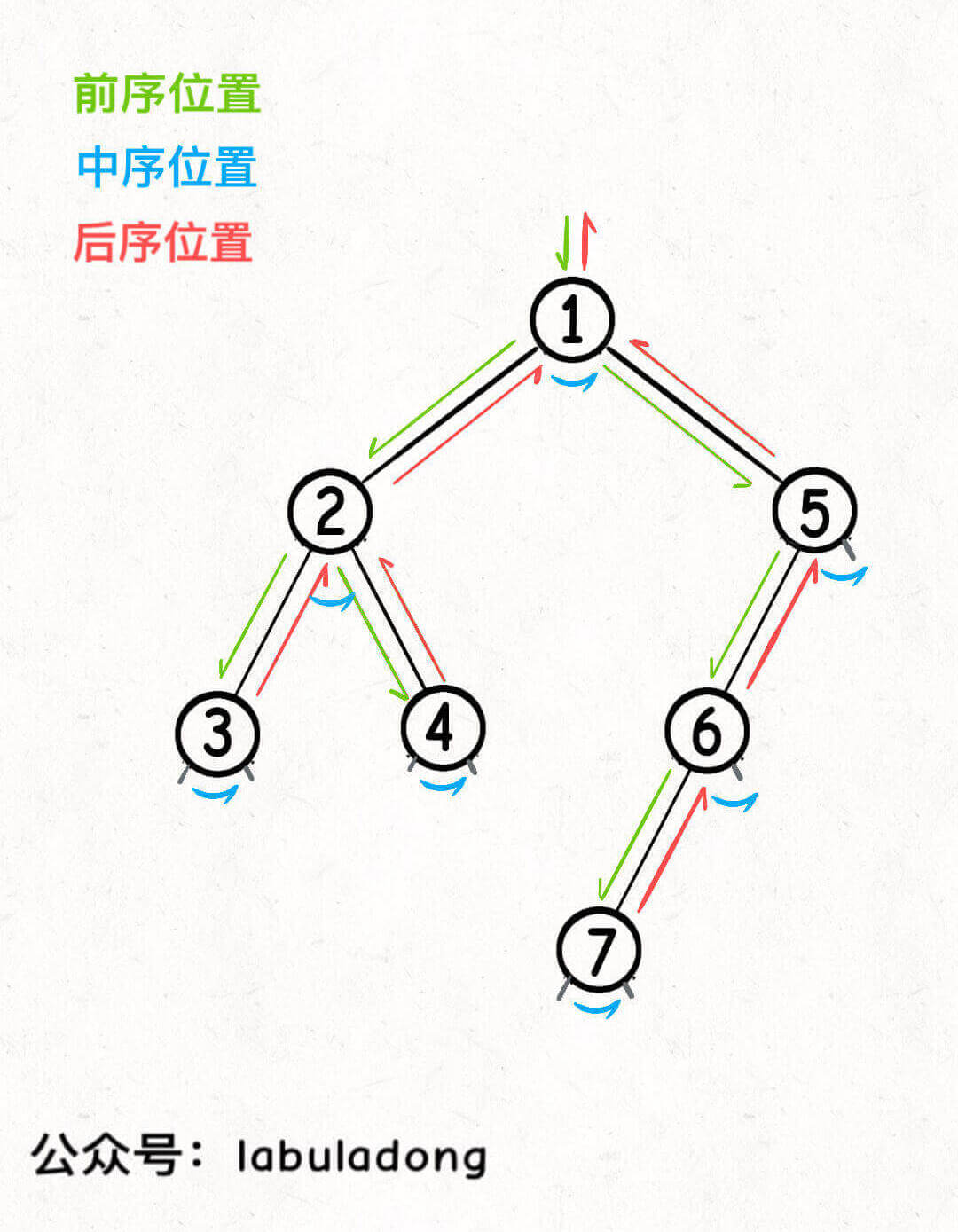
你可以发现每个节点都有「唯一」属于自己的前中后序位置，所以我说前中后序遍历是遍历二叉树过程中处理每一个节点的三个特殊时间点。

这里你也可以理解为什么多叉树没有中序位置，因为二叉树的每个节点只会进行唯一一次左子树切换右子树，而多叉树节点可能有很多子节点，会多次切换子树去遍历，所以多叉树节点没有「唯一」的中序遍历位置。

说了这么多基础的，就是要帮你对二叉树建立正确的认识，然后你会发现：

二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

两种解题思路

#

**二叉树题目的递归解法可以分两类思路，第一类是遍历一遍二叉树得出答案，第二类是通过分解问题计算出答案，这两类思路分别对应着  [[回溯算法（DFS算法）]]  和  [[动态规划]]。

[!tip]

这里说一下我的函数命名习惯：二叉树中用遍历思路解题时函数签名一般是  void traverse(...)，没有返回值，靠更新外部变量来计算结果，而用分解问题思路解题时函数名根据该函数具体功能而定，而且一般会有返回值，返回值是子问题的计算结果。

与此对应的，你会发现我在  [[回溯算法（DFS算法）]]  中给出的函数签名一般也是没有返回值的  void backtrack(...)，而在  [[动态规划]]  中给出的函数签名是带有返回值的  dp  函数。这也说明它俩和二叉树之间千丝万缕的联系。

虽然函数命名没有什么硬性的要求，但我还是建议你也遵循我的这种风格，这样更能突出函数的作用和解题的思维模式，便于你自己理解和运用。

当时我是用二叉树的最大深度这个问题来举例，重点在于把这两种思路和动态规划和回溯算法进行对比，而本文的重点在于分析这两种思路如何解决二叉树的题目。

力扣第 104 题「二叉树的最大深度」就是最大深度的题目，所谓最大深度就是根节点到「最远」叶子节点的最长路径上的节点数，比如输入这棵二叉树，算法应该返回 3：

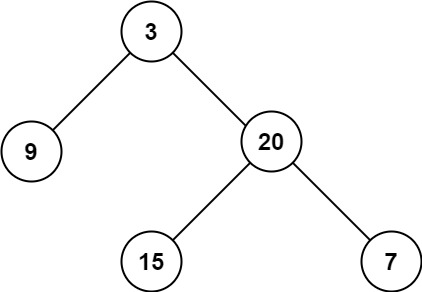
你做这题的思路是什么？显然遍历一遍二叉树，用一个外部变量记录每个节点所在的深度，取最大值就可以得到最大深度，这就是遍历二叉树计算答案的思路。

解法代码如下：

class Solution:
    def __init__(self):
        # 记录最大深度
        self.res = 0
        # 记录遍历到的节点的深度
        self.depth = 0

    def maxDepth(self, root: TreeNode) -> int:
        self.traverse(root)
        return self.res

    # 二叉树遍历框架
    def traverse(self, root: TreeNode) -> None:
        if root is None:
            return
        # 前序位置
        self.depth += 1
        if root.left is None and root.right is None:
            # 到达叶子节点，更新最大深度
            self.res = max(self.res, self.depth)
        self.traverse(root.left)
        self.traverse(root.right)
        # 后序位置
        self.depth -= 1

这个解法应该很好理解，但为什么需要在前序位置增加  depth，在后序位置减小  depth？

因为前面说了，前序位置是进入一个节点的时候，后序位置是离开一个节点的时候，depth  记录当前递归到的节点深度，你把  traverse  理解成在二叉树上游走的一个指针，所以当然要这样维护。

至于对  res  的更新，你放到前中后序位置都可以，只要保证在进入节点之后，离开节点之前（即  depth  自增之后，自减之前）就行了。

当然，你也很容易发现一棵二叉树的最大深度可以通过子树的最大深度推导出来，这就是分解问题计算答案的思路。

解法代码如下：

class Solution:
    # 定义：输入根节点，返回这棵二叉树的最大深度
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        # 利用定义，计算左右子树的最大深度
        leftMax = self.maxDepth(root.left)
        rightMax = self.maxDepth(root.right)
        # 整棵树的最大深度等于左右子树的最大深度取最大值，
        # 然后再加上根节点自己
        res = max(leftMax, rightMax) + 1

        return res

只要明确递归函数的定义，这个解法也不难理解，但为什么主要的代码逻辑集中在后序位置？

因为这个思路正确的核心在于，你确实可以通过子树的最大深度推导出原树的深度，所以当然要首先利用递归函数的定义算出左右子树的最大深度，然后推出原树的最大深度，主要逻辑自然放在后序位置。

如果你理解了最大深度这个问题的两种思路，那么我们再回头看看最基本的二叉树前中后序遍历，就比如力扣第 144 题「二叉树的前序遍历」，让你计算前序遍历结果。

我们熟悉的解法就是用「遍历」的思路，我想应该没什么好说的：

class Solution:
    def __init__(self):
        self.res = []

    # 返回前序遍历结果
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        self.traverse(root)
        return self.res

    # 二叉树遍历函数
    def traverse(self, root: TreeNode):
        if root is None:
            return
        # 前序位置
        self.res.append(root.val)
        self.traverse(root.left)
        self.traverse(root.right)

但你是否能够用「分解问题」的思路，来计算前序遍历的结果？

换句话说，不要用像  traverse  这样的辅助函数和任何外部变量，单纯用题目给的  preorderTraverse  函数递归解题，你会不会？

我们知道前序遍历的特点是，根节点的值排在首位，接着是左子树的前序遍历结果，最后是右子树的前序遍历结果：

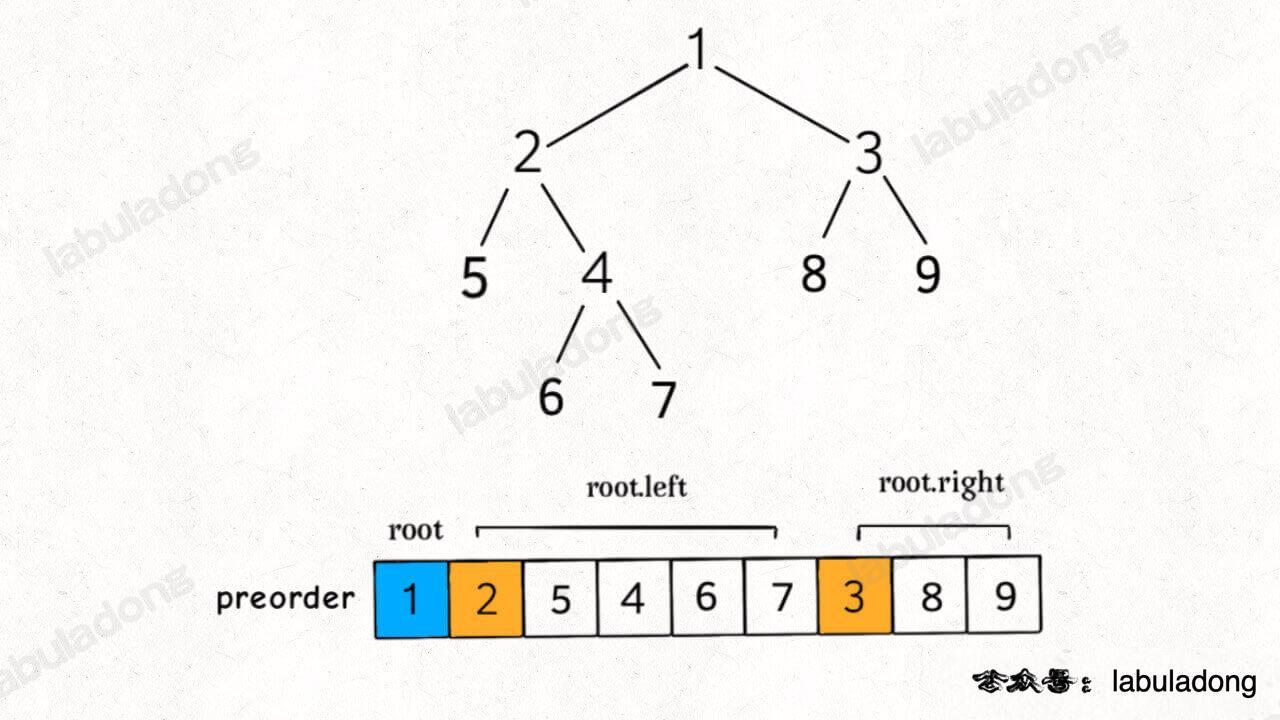
那这不就可以分解问题了么，一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果。

所以，你可以这样实现前序遍历算法：

class Solution:
    # 定义：输入一棵二叉树的根节点，返回这棵树的前序遍历结果
    def preorderTraversal(self, root):
        res = []
        if root == None:
            return res
        # 前序遍历的结果，root.val 在第一个
        res.append(root.val)
        # 利用函数定义，后面接着左子树的前序遍历结果
        res.extend(self.preorderTraversal(root.left))
        # 利用函数定义，最后接着右子树的前序遍历结果
        res.extend(self.preorderTraversal(root.right))
        return res

中序和后序遍历也是类似的，只要把  add(root.val)  放到中序和后序对应的位置就行了。

综上，遇到一道二叉树的题目时的通用思考过程是：

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个  traverse  函数配合外部变量来实现。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。

3、无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

后序位置的特殊之处

#

说后序位置之前，先简单说下前序和中序。

前序位置本身其实没有什么特别的性质，之所以你发现好像很多题都是在前序位置写代码，实际上是因为我们习惯把那些对前中后序位置不敏感的代码写在前序位置罢了。

中序位置主要用在 BST 场景中，你完全可以把 BST 的中序遍历认为是遍历有序数组。

[!tip]+ 划重点

仔细观察，前中后序位置的代码，能力依次增强。

前序位置的代码只能从函数参数中获取父节点传递来的数据。

中序位置的代码不仅可以获取参数数据，还可以获取到左子树通过函数返回值传递回来的数据。

后序位置的代码最强，不仅可以获取参数数据，还可以同时获取到左右子树通过函数返回值传递回来的数据。

所以，某些情况下把代码移到后序位置效率最高；有些事情，只有后序位置的代码能做。

举些具体的例子来感受下它们的能力区别。现在给你一棵二叉树，我问你两个简单的问题：

1、如果把根节点看做第 1 层，如何打印出每一个节点所在的层数？

2、如何打印出每个节点的左右子树各有多少节点？

第一个问题可以这样写代码：

# 二叉树遍历函数
def traverse(root, level):
    if root is None:
        return
    # 前序位置
    print(f"Node {root.val} at level {level}")
    traverse(root.left, level + 1)
    traverse(root.right, level + 1)

# 这样调用
traverse(root, 1)

第二个问题可以这样写代码：

# 定义：输入一棵二叉树，返回这棵二叉树的节点总数
def count(root):
    if root is None:
        return 0
    leftCount = count(root.left)
    rightCount = count(root.right)
    # 后序位置
    print(f"节点 {root} 的左子树有 {leftCount} 个节点，右子树有 {rightCount} 个节点")

    return leftCount + rightCount + 1

这两个问题的根本区别在于

一个节点在第几层，你从根节点遍历过来的过程就能顺带记录，用递归函数的参数就能传递下去；而以一个节点为根的整棵子树有多少个节点，你必须遍历完子树之后才能数清楚，然后通过递归函数的返回值拿到答案。

结合这两个简单的问题，你品味一下后序位置的特点，只有后序位置才能通过返回值获取子树的信息。

那么换句话说，一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

接下来看下后序位置是如何在实际的题目中发挥作用的，简单聊下力扣第 543 题「二叉树的直径」，让你计算一棵二叉树的最长直径长度。

所谓二叉树的「直径」长度，就是任意两个结点之间的路径长度。最长「直径」并不一定要穿过根结点，比如下面这棵二叉树：

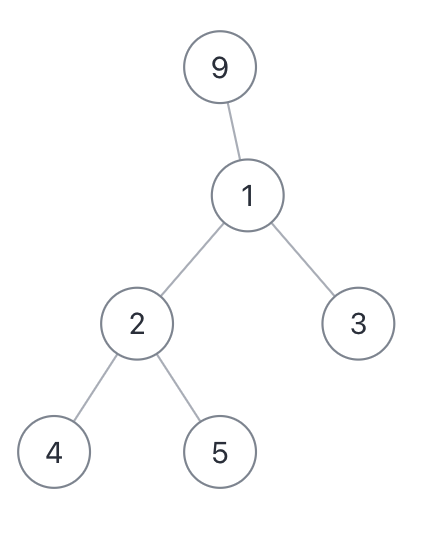
它的最长直径是 3，即  [4,2,1,3]，[4,2,1,9]  或者  [5,2,1,3]  这几条「直径」的长度。

解决这题的关键在于，每一条二叉树的「直径」长度，就是一个节点的左右子树的最大深度之和。

现在让我求整棵树中的最长「直径」，那直截了当的思路就是遍历整棵树中的每个节点，然后通过每个节点的左右子树的最大深度算出每个节点的「直径」，最后把所有「直径」求个最大值即可。

最大深度的算法我们刚才实现过了，上述思路就可以写出以下代码：

class Solution:

    def __init__(self):
        # 记录最大直径的长度
        self.maxDiameter = 0

    def diameterOfBinaryTree(self, root):
        # 对每个节点计算直径，求最大直径
        self.traverse(root)
        return self.maxDiameter

    # 遍历二叉树
    def traverse(self, root):
        if root is None:
            return
        # 对每个节点计算直径
        leftMax = self.maxDepth(root.left)
        rightMax = self.maxDepth(root.right)
        myDiameter = leftMax + rightMax
        # 更新全局最大直径
        self.maxDiameter = max(self.maxDiameter, myDiameter)

        self.traverse(root.left)
        self.traverse(root.right)

    # 计算二叉树的最大深度
    def maxDepth(self, root):
        if root is None:
            return 0
        leftMax = self.maxDepth(root.left)
        rightMax = self.maxDepth(root.right)
        return 1 + max(leftMax, rightMax)

这个解法是正确的，但是运行时间很长，原因也很明显，traverse  遍历每个节点的时候还会调用递归函数  maxDepth，而  maxDepth  是要遍历子树的所有节点的，所以最坏时间复杂度是 O(N^2)。

这就出现了刚才探讨的情况，前序位置无法获取子树信息，所以只能让每个节点调用  maxDepth  函数去算子树的深度。

那如何优化？我们应该把计算「直径」的逻辑放在后序位置，准确说应该是放在  maxDepth  的后序位置，因为  maxDepth  的后序位置是知道左右子树的最大深度的。

所以，稍微改一下代码逻辑即可得到更好的解法：

class Solution:
    def __init__(self):
        # 记录最大直径的长度
        self.maxDiameter = 0

    def diameterOfBinaryTree(self, root):
        self.maxDepth(root)
        return self.maxDiameter

    def maxDepth(self, root):
        if root is None:
            return 0
        leftMax = self.maxDepth(root.left)
        rightMax = self.maxDepth(root.right)
        # 后序位置，顺便计算最大直径
        myDiameter = leftMax + rightMax
        self.maxDiameter = max(self.maxDiameter, myDiameter)

        return 1 + max(leftMax, rightMax)

这下时间复杂度只有  maxDepth  函数的 O(N) 了。

讲到这里，照应一下前文：遇到子树问题，首先想到的是给函数设置返回值，然后在后序位置做文章。

[!tip] 利用后序位置的题目，一般都使用「分解问题」的思路。因为当前节点接收并利用了子树返回的信息，这就意味着你把原问题分解成了当前节点 + 左右子树的子问题。

反过来，如果你写出了类似一开始的那种递归套递归的解法，大概率也需要反思是不是可以通过后序遍历优化了。

以树的视角看动归/回溯/DFS 算法的区别和联系

#

前文我说动态规划/回溯算法就是二叉树算法两种不同思路的表现形式，相信能看到这里的读者应该也认可了我这个观点。但有细心的读者经常提问：你的思考方法让我豁然开朗，但你好像一直没讲过 DFS 算法？

因为 DFS 算法和回溯算法非常类似，只是在细节上有所区别。

这个细节上的差别是什么呢？其实就是「做选择」和「撤销选择」到底在 for 循环外面还是里面的区别，DFS 算法在外面，回溯算法在里面。

为什么有这个区别？还是要结合着二叉树理解。这一部分我就把回溯算法、DFS 算法、动态规划三种经典的算法思想，以及它们和二叉树算法的联系和区别，用一句话来说明：

[!note]+ 划重点

动归/DFS/回溯算法都可以看做二叉树问题的扩展，只是它们的关注点不同：

• 动态规划算法属于分解问题（分治）的思路，它的关注点在整棵「子树」。
• 回溯算法属于遍历的思路，它的关注点在节点间的「树枝」。
• DFS 算法属于遍历的思路，它的关注点在单个「节点」。

怎么理解？我分别举三个例子你就懂了。

例子一：分解问题的思想体现

#

第一个例子，给你一棵二叉树，请你用分解问题的思路写一个  count  函数，计算这棵二叉树共有多少个节点。代码很简单，上文都写过了：

# 定义：输入一棵二叉树，返回这棵二叉树的节点总数
def count(root):
    if root is None:
        return 0
    # 当前节点关心的是两个子树的节点总数分别是多少
    # 因为用子问题的结果可以推导出原问题的结果
    leftCount = count(root.left)
    rightCount = count(root.right)
    # 后序位置，左右子树节点数加上自己就是整棵树的节点数
    return leftCount + rightCount + 1

你看，这就是动态规划分解问题的思路，它的着眼点永远是结构相同的整个子问题，类比到二叉树上就是「子树」。

例子二：回溯算法的思想体现

#

第二个例子，给你一棵二叉树，请你用遍历的思路写一个  traverse  函数，打印出遍历这棵二叉树的过程，你看下代码：

def traverse(root):
    if root is None:
        return
    print("从节点 %s 进入节点 %s" %(root, root.left))
    traverse(root.left)
    print("从节点 %s 回到节点 %s" %(root.left, root))

    print("从节点 %s 进入节点 %s" %(root, root.right))
    traverse(root.right)
    print("从节点 %s 回到节点 %s" %(root.right, root))

不难理解吧，好的，我们现在从二叉树进阶成多叉树，代码也是类似的：

# 多叉树节点
class Node:
    def __init__(self, val=0, children=None):
        self.val = val
        self.children = children if children is not None else []

def traverse(root):
    if not root: return
    for child in root.children:
        print(f"从节点 {root} 进入节点 {child}")
        traverse(child)
        print(f"从节点 {child} 回到节点 {root}")

这个多叉树的遍历框架就可以延伸出  [[回溯算法（DFS算法）]]中的回溯算法框架：

// 回溯算法框架
void backtrack(...) {
    // base case
    if (...) return;

    for (int i = 0; i < ...; i++) {
        // 做选择
        ...

        // 进入下一层决策树
        backtrack(...);

        // 撤销刚才做的选择
        ...
    }
}

你看，这就是回溯算法遍历的思路，它的着眼点永远是在节点之间移动的过程，类比到二叉树上就是「树枝」。

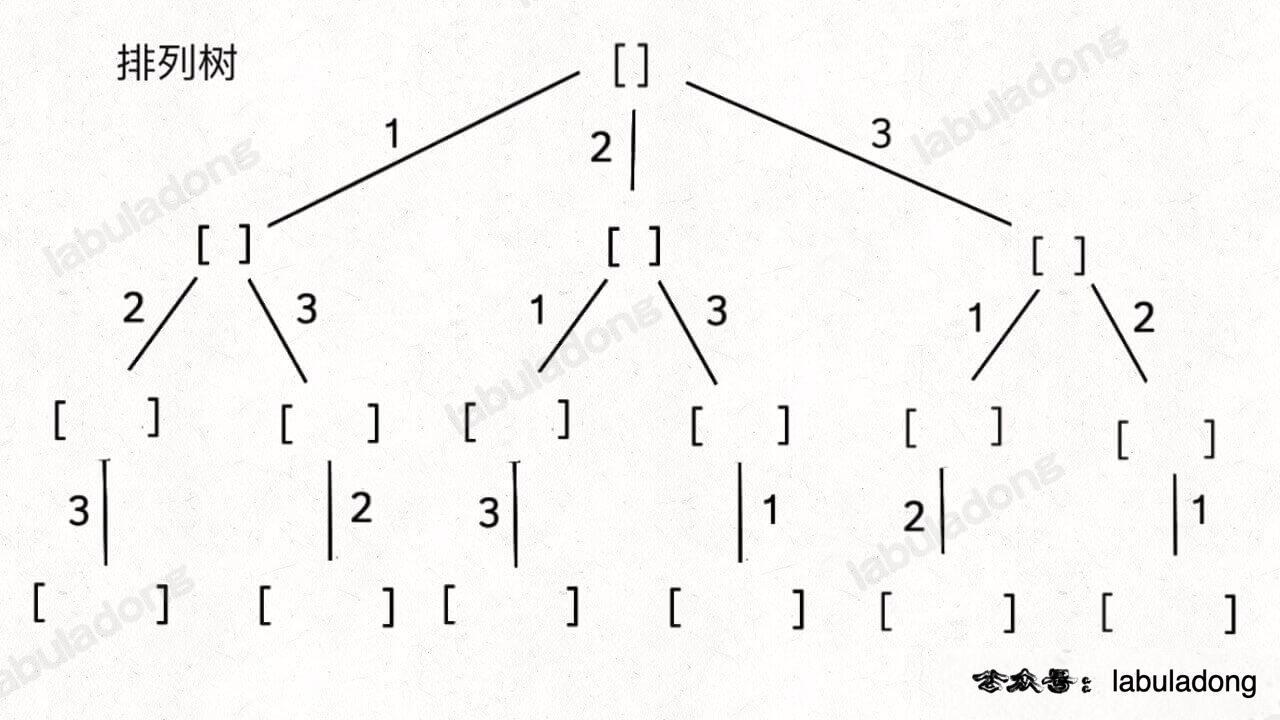
你再看看具体的回溯算法问题，我们的关注点在一条条树枝上：

// 回溯算法核心部分代码
void backtrack(int[] nums) {
    // 回溯算法框架
    for (int i = 0; i < nums.length; i++) {
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        // 进入下一层回溯树
        backtrack(nums);

        // 取消选择
        track.removeLast();
        used[i] = false;
    }
}

例子三：DFS 的思想体现

#

第三个例子，我给你一棵二叉树，请你写一个  traverse  函数，把这棵二叉树上的每个节点的值都加一。很简单吧，代码如下：

def traverse(root):
    if root is None:
        return
    # 遍历过的每个节点的值加一
    root.val += 1
    traverse(root.left)
    traverse(root.right)

你看，这就是 DFS 算法遍历的思路，它的着眼点永远是在单一的节点上，类比到二叉树上就是处理每个「节点」。